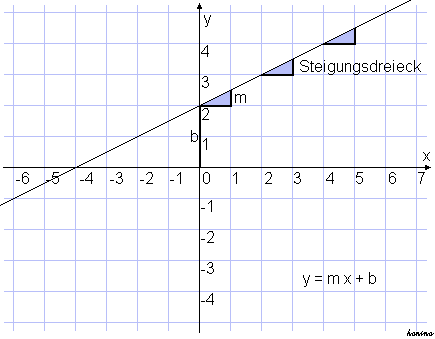Funktionale Zusammenhänge - Spezielle Funktionen
| Lineare Funktion |
Quelle: Honina (2017): Lineare Funktion.- Web: https://upload.wikimedia.org/wikipedia/commons/e/ee/Linear_Function.png (1.2.2018) üblicherweise: f(x) = k*x + d mit der Steigung k und dem y-Achsenabschnitt d = f(0) Das Steigungsdreieck kann beliebig breit eingezeichnet werden. Die Steigung bezeichnet das Verhältnis der beiden Katheten (Seiten, die einen rechten Winkel bilden) dieses Dreiecks. Wenn die horizontale Kathete die Einheit 1 ist, dann entspricht die zweite Kathete dem Steigungswert. |
|
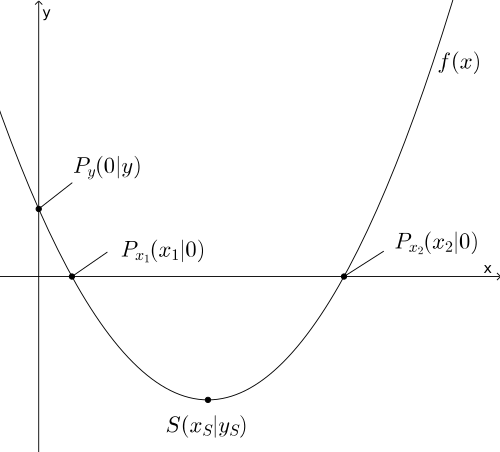
Quadratische Funktion |
Quelle: Kmhkmh (2017) Quadratische Funktion.- Web: https://upload.wikimedia.org/wikipedia/commons/c/ce/Quadratische_funktion.svg (1.2.2018) üblicherweise: f(x) = x² oder f(x) = a * xb oder f(x) = a * (x-b)c Die Steigung der quadratischen Funktion variiert; je weiter nach rechts, desto steiler wird die Funktion, desto größer ist die Steigung (falls a > 1). Je größer der Exponent c, desto steiler wird die Funktion. |
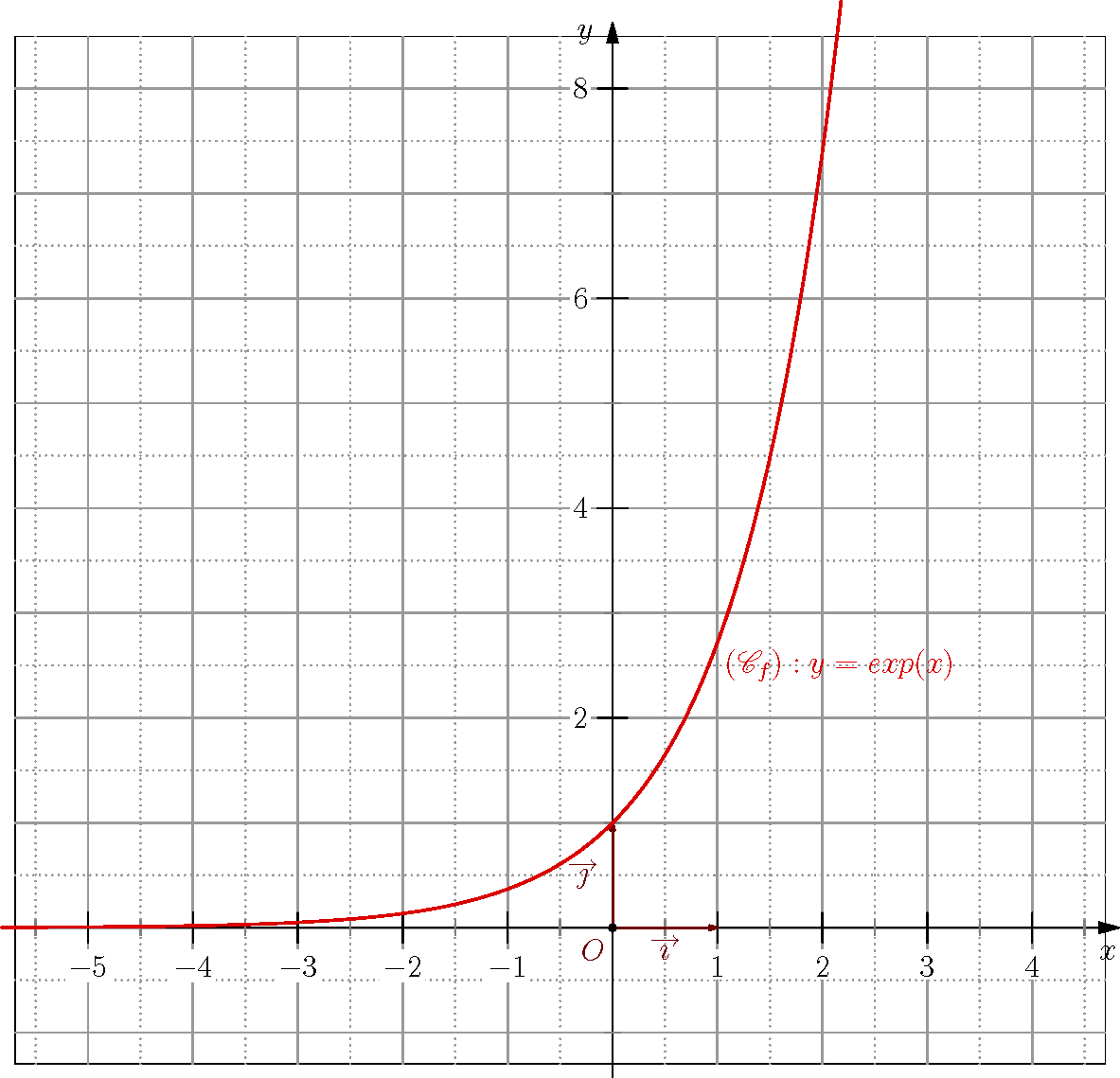
| Exponentielle Funktion |
Quelle: Shaoren (2008): Exponentielle Funktion.- Web: https://upload.wikimedia.org/wikipedia/commons/0/06/Fonction_repr%C3%A9sentative_de_la_fonction_exponentielle.png (1.2.2018) üblicherweise: f(x) = ex oder f(x) = exp(x) oder f(x) = ax Die Steigung der Funktion steigt (ab einer gewissen Stelle) schneller an als bei quadratischen Funktionen (Polynomfunktionen) |
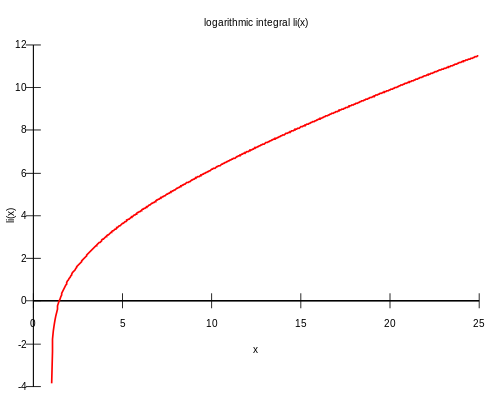
| Logarithmische Funktion |
Quelle: Maksim (2006): Logarithmische Funktion. Web: https://commons.wikimedia.org/wiki/File:Logarithmic_integral.svg (1.2.2018) üblicherweise f(x) = log(x) oder f(x) = ln(x) oder f(x) = alog(x) Die Steigung der Logarithmusfunktion wird immer geringer; je weiter nach rechts, desto kleiner ist die Steigung, sie bleibt aber immer größer als 0. |
|
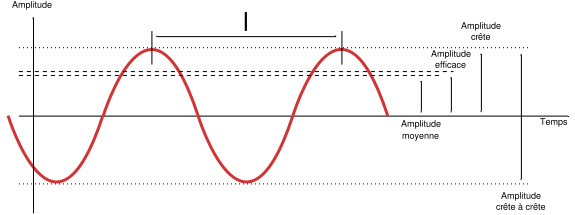
Winkelfunktionen Sinus, Cosinus |
Quelle: Qualc1 (2006): Sinusfunktion. Web: https://commons.wikimedia.org/wiki/File:Sinus_amplitude.svg (1.2.2018) Periodisch wiederkehrende Ereignisse werden mit Winkelfunktionen wie Sinus oder Cosinus beschrieben. üblicherweise f(x) = sin(x) oder f(x) = cos (x) oder f(x) = a * sin(x-b) Die Steigung wird einmal größer, erreicht einen Maximalwert, sinkt wieder ab. Sie erreicht im Maximum (= dem höchsten Funktionswert) den Wert 0, wird anschließend negativ. Sie erreicht einen Minimalwert und ist im Minimum (= dem kleinsten Funktionswert) wiederum den Wert 0. |