Kursthemen
-
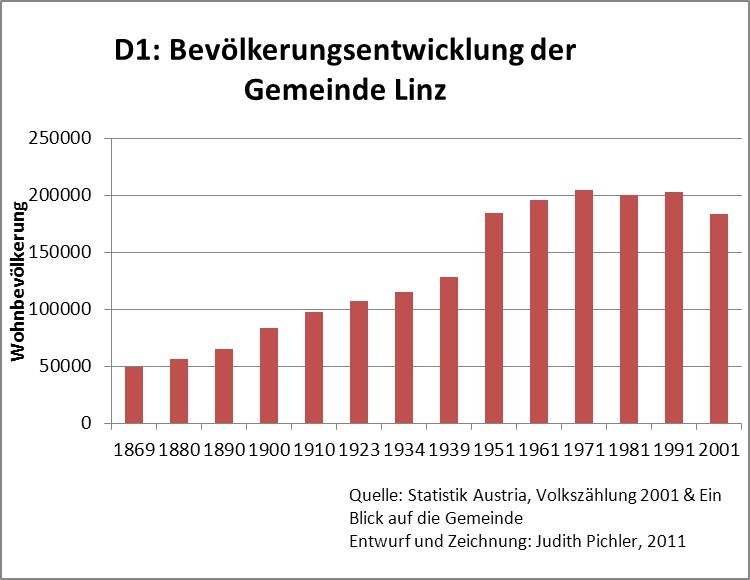
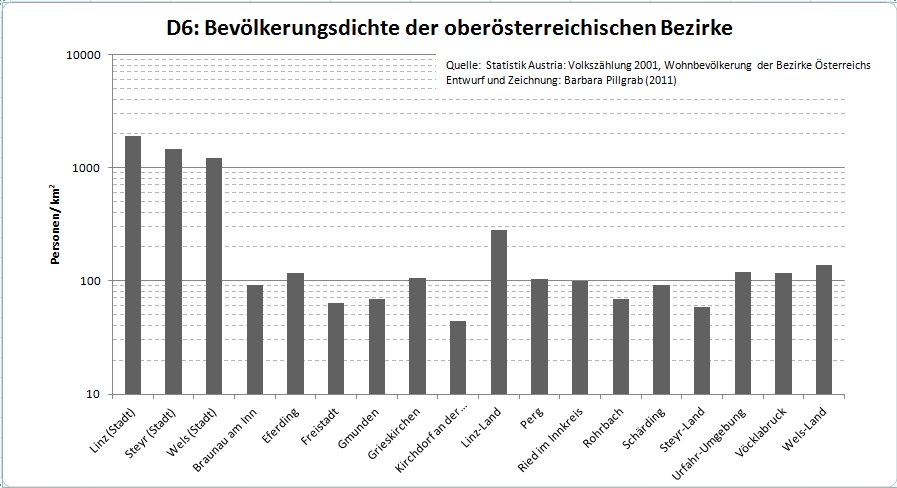
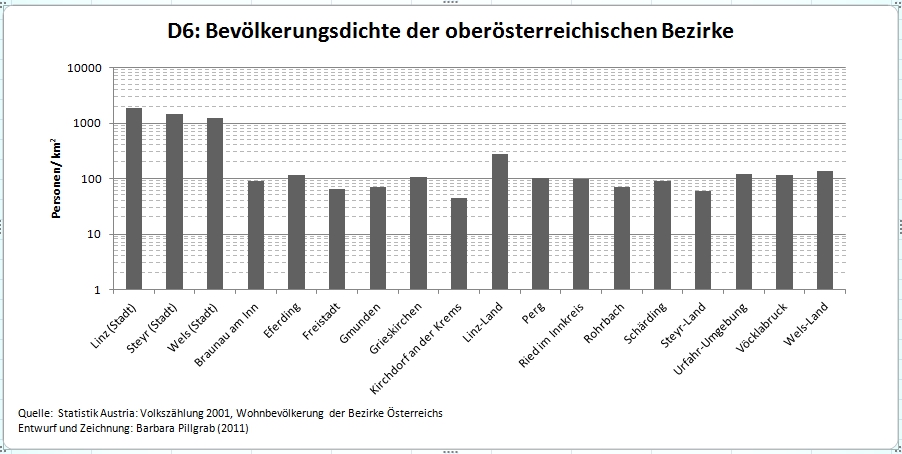
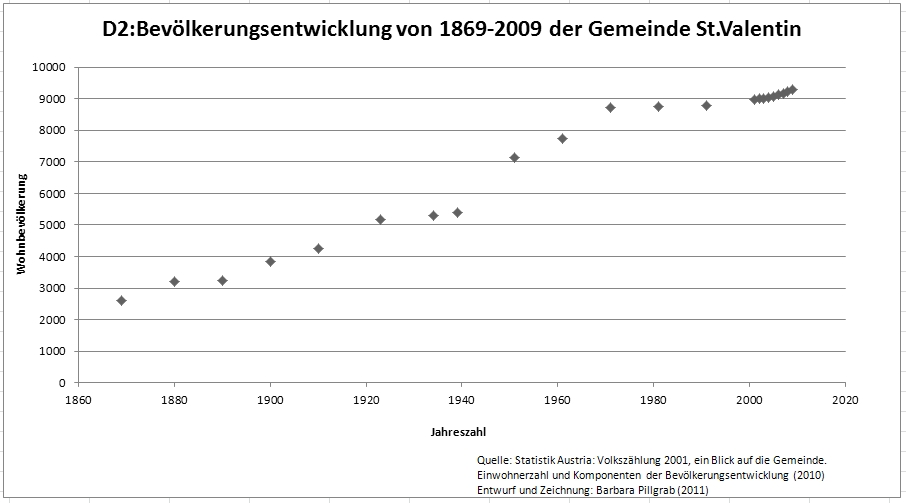
Visualisierung in Diagrammen
-
-
-
- Je höher der Wert, desto länger die Säule. Dabei werden die Werte auf der y-Achse i. a. in einem linearen Maßstab aufgetragen. Die Änderung des Datenwertes um eine bestimmte Größe entspricht an jedem Punkt der y-Achse der gleichen Änderung der Stablänge. Die Beschriftung der y-Achse gibt das Merkmal und die Einheit an.
Der kleinste Wert ist in der Regel 0, der größte richtet sich je nach Datenlage; beide können über die Achseneigenschaften manuell eingestellt werden.
- Je höher der Wert, desto länger die Säule. Dabei werden die Werte auf der y-Achse i. a. in einem linearen Maßstab aufgetragen. Die Änderung des Datenwertes um eine bestimmte Größe entspricht an jedem Punkt der y-Achse der gleichen Änderung der Stablänge. Die Beschriftung der y-Achse gibt das Merkmal und die Einheit an.
-
- Alternativ dazu wird bei extremen Größenunterschieden auf der y-Achse ein logarithmischer Maßstab verwendet. Der Abstand zwischen zwei Einheiten auf der y-Achse entspricht dann in der Regel dem zehnfachen Wert der vorhergehenden Einheit. Prinzipiell wäre auch eine andere Basis als ein Zehnerlogarithmus denkbar, das ist aber unüblich.
-
-
Zur Darstellung von (zeitlichen) Entwicklungen werden oft Punkt- oder Liniendiagramme verwendet. Dabei muss beim (auf der x-Achse) dargestellten Merkmal eine Größenbeziehung möglich sein ("Ordinalskala" oder "Kardinalskala").
- Üblicherweise steht in jenen Regionen der Welt, in denen von links nach rechts geschrieben wird, der kleinste Wert auf der x-Achse links und der größte rechts. Die y-Achse befindet sich üblicherweise am linken Diagrammrand.
-
- Um die Entwicklung besser sichtbar zu machen, werden die Datenpunkte oft (geradlinig) verbunden, sodass eine Polygonlinie entsteht. Dies ist jedoch nur bei einer hohen Anzahl von Werten (auf der x-Achse) sinnvoll (ein nahezu "stetiges" Merkmal). Ein Ablesen von Werten zwischen den Datenpunkten ist nicht zulässig.
- Ein Verbinden der Datenpunkte durch eine gekrümmte (gebogene, geschweifte) Linie ist in der Regel unzulässig, weil es eine höhere Datenhäufigkeit vermuten lässt und zum Ablesen von Zwischenwerten einlädt.
-
-
-
Zur Visualisierung von relativen Größen werden oft Kreisdiagramme verwendet. Damit kann die "Verteilung", die strukturelle Zusammensetzung einer Gesamtgröße leichter erkannt werden.
-
-
-
Sollen verschiedene Merkmale oder Merkmale mit extrem unterschiedlichen Werten in einem Diagramm dargestellt werden, kann man zur Visualisierung
- für ein Merkmal eine zweite y-Achse am rechten Diagrammrand verwenden. Zur klaren Kennzeichnung wäre eine Kombination zweiter Diagrammarten sinnvoll (Stab- und Liniendiagramm).
- einen logarithmischen Maßstab verwenden.
Im schulischen Kontext ist die Verwendung zweier getrennter Diagramme empfehlenswert.
-
Ein ähnliches kombiniertes Diagramm wäre das klassische Klimadiagramm nach Walther-Lieth. Die Temperatur wird auf der linken y-Achse, der Niederschlag auf der rechten y-Achse dargestellt. Dabei haben sie gleiche Nulllinie und ein Zahlenerhältnis von 1 : 2 (10° Celsius entsprechen 20 mm Niederschlag).
In Tabellenkalkulationen kann das durch passendes Einstellen der Minimum- und Maximumwerte auf beiden Achsen erreicht werden. Der übliche Maßstabsbruch bei 100 mm Niederschlag kann dabei nicht dargestellt werden.
-
-
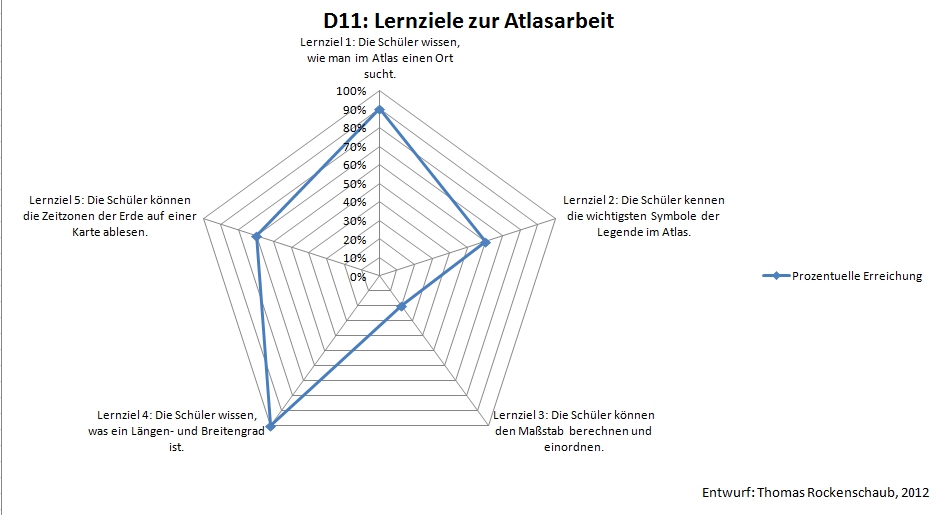
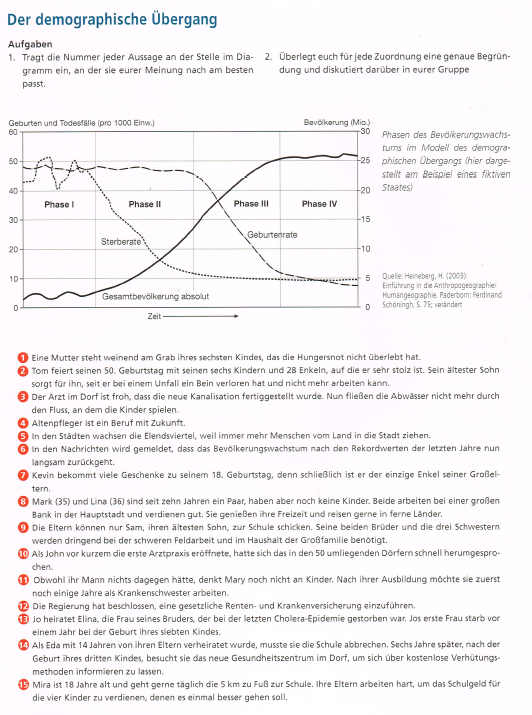
Für bestimme Sachverhalte werden Netzwerkdiagramme verwendet. Dies ist beispielsweise bei intervallskalierten Merkmalen wie Windrichtungen oder nomialskalierten Merkmalen wie Lernzielen sinnvoll, vor allem, wenn ein Vergleich zwischen den einzelnen Merkmalen gezogen werden soll.
-
-
-
Claudia Breifuss (2020): Präsentation: Diagramme und Klimadiagramme im GW-Unterricht.- Linz.
Web: https://gwb.schule.at/mod/resource/view.php?id=21795 (6.5.2020) -
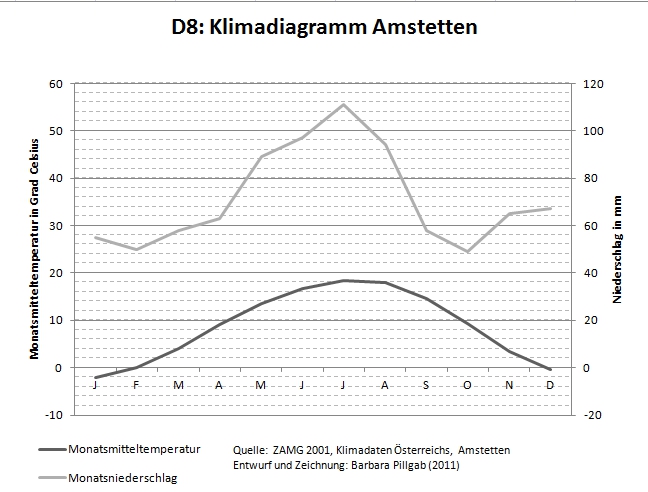
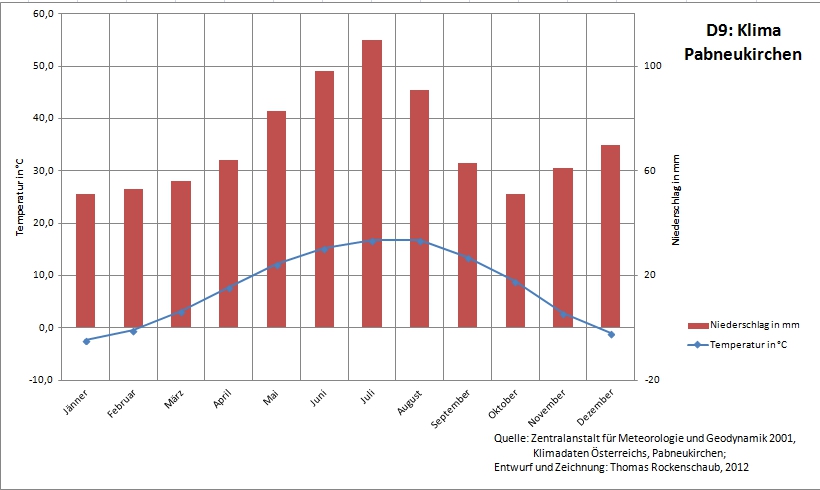
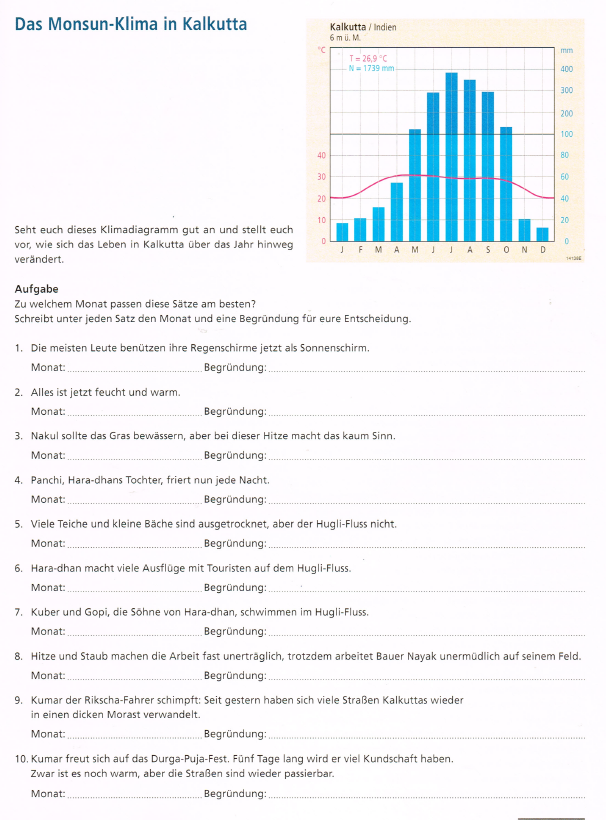
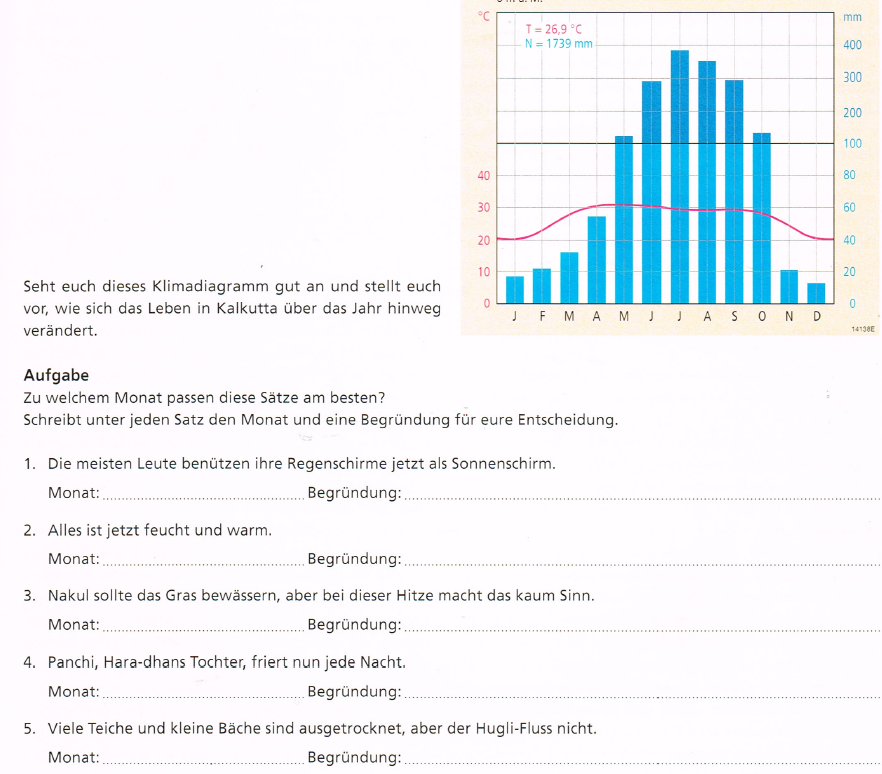
- Klassischer Aufgabentyp (bis 2005): "Interpretiere das Klimadiagramm"
- Aktueller Aufgabentyp nach Anforderungsbereiche:
- "Beschreibe das Klima von ... mit Hilfe des Diagramms." (AFB I)
- "Vergleiche das Klima von A mit B mit Hilfe der beiden Diagramme." (AFB II)
- "Erörtere das Klima im Zusammenhang mit Monsuneffekten," (AFB II)
- "Nimm Stellung zur Wahl eines Zeitpunktes, wann du diese Region als Tourist besuchn willst. Was musst du einpacken, damit du für das zu erwartende Wetter gut gerüstet bist?" (AFB III)
-
- Aufgabentyp mit geschlossenen Aufgabestellungen
-
-
-
Klicken Sie auf den Link und gehen Sie zum aufklappbaren Menüpunkt weiterführende Daten > weiter zu StatCube > wählen Sie dort den Link STATcube: Bevölkerung seit 1869 nach Gemeinden
*neues Fenster*
Melden Sie sich als Gast (Nutzungsbedingungen müssen akzeptiert werden) an > vor Ihnen öffnet sich eine Tabelle mit den Bundesländern. Klicken Sie auf ein Bundesland > klicken Sie auf einen Bezirk > klicken Sie Daten abrufen in der Menüleiste (links oben) > klicken Sie auf Tabelle herunterladen (rechts oben)
-
Klicken Sie auf den Link > vor Ihnen öffnet sich eine Tabelle mit den Bundesländern. Klicken Sie auf ein Bundesland > klicken Sie Daten abrufen in der Menüleiste (links oben) > klicken Sie auf Tabelle herunterladen (rechts oben)