Zur Grafischen Darstellung von Vektoren
Abschlussbedingungen
Für Vektoren gibt es zwei unterschiedliche Definitionen:
- Ein Vektor ist ein geordnete Liste von Zahlen. Die Bedeutung der Zahlen liegt in der Größe und der Stelle, an der sie steht.
- In diesem Sinne ist ein Vektor eine einfache Form einer Matrix, eine einspaltige Matrix.
- Anwendungsbeispiele wären die Tabelle von Fußballvereinen, eine Messserie von sportlichen Werten, die Messerie eines Maßschneiders, die Koordinaten eines Punktes, die geographischen Koordinaten, ...
- Matrizen spielen eine wesentliche Rolle bei der Verarbeitung von Daten.
- Vektoren können als Pfeile visualisiert werden.
- Ein Vektor ist ein Pfeil mit einem Anfangs- und einem Endpunkt oder einem Anfangspunkt, einer Richtung, einer Orientierung und einer Länge.
- In der Physik (Kräfte, ....) wird vor allem dieses Verständnis verwendet.
- Vektoren können grafisch addiert werden, indem der zweite Pfeil an die Spitze des ersten gesetzt wird. Der Ergebnispfeil (die "Summe"), die Resultierende, geht vom Anfangspunkt des ersten zum Endpunkt des zweiten Pfeils.
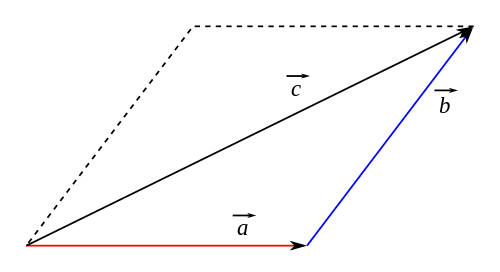
Quelle: Jacek FH (2007): Vektoraddition. Web: https://commons.wikimedia.org/wiki/File:Wektory_sumt.svg (1.2.2018)
Zuletzt geändert: Donnerstag, 1. Februar 2018, 07:01