Winkelfunktionen
Winkelfunktionen werden vom Kreis (EInheitskreis) abgeleitet und haben typische Bilder.
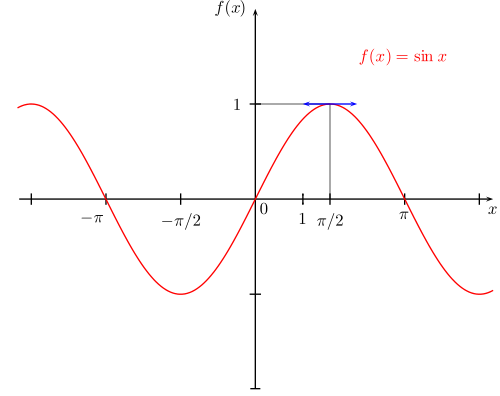
| Sinus-Funktion |
Quelle: Quark67 (2013): Sinus-Funktion.- Web: https://commons.wikimedia.org/wiki/File:Sinus.svg (1.2.2018) Die Sinus-Funktion beschreibt immer wiederkehrende Zusammenhänge. üblicherweise: f(x) = sin(x) oder f(x) = a * sin (x-b) Sie hat einen höchsten Wert (= Maximum) und einen niedrigsten Wert (= Minimum). Ihr Wertebereich liegt i. A. zwischen -1 und +1. Der Abschnitt, der sich wiederholt, wird als Periode bezeichnet; üblicherweies 2*Pi also 360°, der Umfang eines Kreises. |
| Cosinus-Funktion |
Die Cosinus-Funktion entspricht der Sinus-Funktion, nur um 90° oder Pi/2 verschoben. üblicherweise: f(x) = cos(x) |
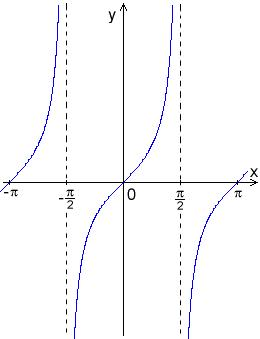
| Tangens-Funktion |
Quelle: Pajs (2006): Tangens-Funktion. Web: https://upload.wikimedia.org/wikipedia/commons/7/79/Graf_tangens.png (1.2.2018) Eine periodisch wiederkehrende Funktion mit der größten Steigung im Nullpunkt. üblicherweise: f(x) = tan(x) oder f(x) = a * tan(x-b) |
| Cotangens-Funktion |
Die Cotangens-Funktion entspricht der Tangensfunktion, nur um 90° oder Pi/2 verschoben. f(x) = cot(x) |
| Arcus-Funktionen |
Die Arcus-Funktionen sind die Umkehr-Funktionen der Winkelfunktionen. Ist der Funktionswert gegeben, kann daraus der x-Wert (die Stelle) bestimmt werden. f(x) = sin(x) führt zu x = arcsin[ f(x) ] |