Definitionen
Definition 2-10:
Unter der Spannweite (Variationsbreite, engl. range) w versteht man die Differenz zwischen größtem und kleinstem Merkmalswert.
Beispiel:
Definition 2-11:
Unter der Varianz (engl. variance) s2 einer Stichprobe x1, x2, ... xn mit Mittelwert x-quer versteht man 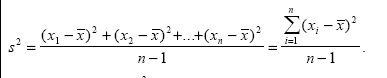
Unter der Varianz σ2 der Population X mit den Ausprägungen x1 bis xn und dem Mittelwert μ versteht man 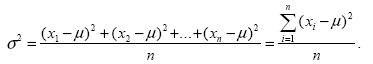
Definition 2-12:
Die Standardabweichung (engl. standard deviation) ist gleich der Wurzel aus der Varianz.
Theorem 2-7: (ohne Beweis)
Kommen die k verschiedenen Merkmalsausprägungen x1, x2, ... xk einer Variablen X mit den absoluten Häufigkeiten h1, h2, ... hk vor, so gilt für die Varianz
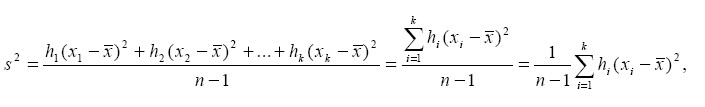
Beispiel:
Definition 2-13:
Der Variationskoeffizient (Abweichungskoeffizient) ist im Gegensatz zu Standardabweichung/Varianz ein relatives Streuungsmaß. Das bedeutet, er hängt nicht von der Maßeinheit der Variable ab und ist somit dimensionslos. Ziel ist es, eine Einordnung und Vergleichbarkeit der Varianz durch Normierung zu erreichen (s. Formel).
Ein Beispiel für die Anwendung des Variationskoeffizienten ist der Vergleich der Streuung (Standardabweichung) von zwei Datensätzen:
- Preis von verkauften Smartphones im letzten Jahr (Annahme: x̄ = 300; s = 160)
- Preis von verkauften Autos im letzten Jahr (Annahme: x̄ = 30.000; s = 16.000)
Durch die sehr unterschiedlichen Absolutwerte sind die Standardabweichungen der beiden Variablen nicht direkt vergleichbar. Deshalb wird mit dem Variationskoeffizienten einen Normalisierung über den mittelwert vorgenommen.
Der Variationskoeffizient ist nur sinnvoll für Messreihen mit ausschließlich positiven (oder ausschließlich negativen) Werten.
Formel:
Beispiel: