Beispiele
Beispiel 2-26:
Die unterschiedliche Spendenbereitschaft der Bekannten von Herrn Müller bzw. Herrn Maier (s. Beispiel 2-24) ist durch Varianz und Standardabweichung zu charakterisieren.
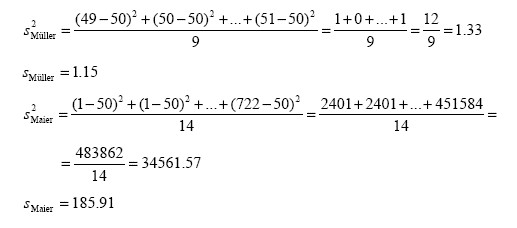
oder
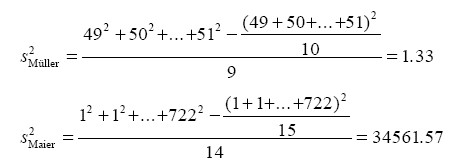
Die beiden Beispiele 2-24 und 2-26 haben die Relevanz des arithmetischen Mittels im Hinblick auf die Charakterisierung einer Häufigkeitsverteilung deutlich erkennen lassen. So ist dieses umso aussagekräftiger, je enger die Werte um den Mittelwert liegen, d. h. je kleiner Varianz bzw. Standardabweichung sind.
Beispiel 2-28:
Es sind Varianz und Standardabweichung der monatlichen Studenteneinkommen zu ermitteln, wobei als Ausgangsbasis die in der beiliegenden Tabelle 2-2c angegebene Häufigkeitstabelle dienen möge.
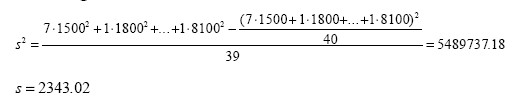
Wie man anhand von Beispielen leicht belegen kann, lässt sich bei Vorliegen gruppierter Daten die Varianz - ebenso wie das arithmetische Mittel - nicht mehr exakt berechnen. Sofern die Merkmalswerte innerhalb der einzelnen Klassen jedoch gleichmäßig verteilt sind, kann die Varianz der gruppierten Daten unter Heranziehung von Definition 2-13 allerdings näherungsweise bestimmt werden. Es ist in diesem Zusammenhang überflüssig, darauf hinzuweisen, dass ein wesentliches Kriterium für die Güte dieser Approximation und somit für die Aussagekraft der Varianz in der Adäquatheit der gewählten Klasseneinteilung liegt.
Beispiel 2-29:
Es sind - ausgehend sowohl von Definition 2-13 als auch von Theorem 2-9 - Varianz und Standardabweichung der monatlichen Studenteneinkommen zu ermitteln, wobei als Ausgangsbasis die in Tabelle 2-3 angegebene klassifizierte Häufigkeitsverteilung dienen möge.
In Beispiel 2-22 hat man für das arithmetische Mittel der gruppierten Daten x_quer = 4375 erhalten.
Für die Varianz der gruppierten Daten gilt somit per definitionem:
.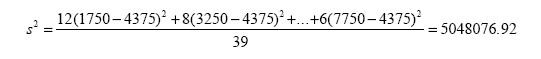
Unter Heranziehung von Theorem 2-9 erhält man für die Varianz denselben Wert, zumal

gilt. In beiden Fällen folgt für die Standardabweichung s = 2246 79 .