Lösung
Übungsarbeit (Bsp.) 2-15: xmod = „ 1750“
Übungsarbeit. 2-11 (2-14):
Variable „Studiendauer“: xmed = 4,5 .
Variable „Kinderzahl“: xmed = 0
Variable „monatliches Einkommen“: xmed = 3750
Übungsarbeit. 2-13:
xmod = „2“ und „4“ (Im vorliegenden Fall ist der Modus nicht eindeutig definiert.)
Übungsarbeit. 2-14:
Die vorliegende Verteilung besitzt keinen Modalwert.
Übungsarbeit. 2-12:
|
|
Variable |
Modus |
Median |
arithm. Mittel |
geom. Mittel |
|
Tab. 3 |
Taschengeld |
50 |
50 |
58,125 |
-- |
|
Tab. 4 |
Mathematiknote |
3,5 |
3 |
-- |
-- |
|
Tab. 5 |
Taschengeld |
62,5 |
62,5 |
60,729 |
-- |
|
Tab. 6 |
Taschengeld |
50 |
50 |
54,375 |
-- |
|
Tab. 7 |
Taschengeld |
50 |
50 |
50,417 |
-- |
Übungsarbeit. 2-20:
Modus: 0
Median: 0
Arithm. Mittel:
1. Variante (ausgehend von der Urliste in Tabelle 2-1)
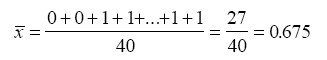
2. Variante (ausgehend von der im Lösungsteil zu Übungsarbeit 2-2 angeführten Häufigkeitstabelle)
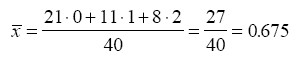
Übungsarbeit. 2-21:
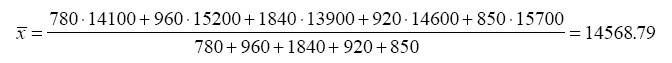
Übungsarbeit. 2-19:
Wie anhand der folgenden Überlegungen gezeigt wird, entspricht die gesuchte durchschnittliche jährliche Zuwachsrate dem geometrischen Mittel der einzelnen Zuwachsraten.
Sofern N1994, N1995, ......., N2000 die Nächtigungszahlen für die Jahre 1994, 1995, ..., 2000 bezeichnen gilt:
N1995 = N1994 . (1 + 0,046)
N1996 = N1995 . (1 + 0,039) = N1994 . (1 + 0,046) . (1 + 0,039)
N1997 = N1996 . (1 + 0,038) = N1994 . (1 + 0,046) . (1 + 0,039) . (1 + 0,038)
......
N2000 = N1999 . (1 + 0,033) = N1994 . (1 + 0,046) . (1 + 0,039) . (1 + 0,038) . (1 + 0,057) .
.(1 + 0,049) . (1 + 0,033)
Für die durchschnittliche Zuwachsrate p gilt: N2000 = N1994 . (1 + p)6
Durch Gleichsetzen erhält man somit
N1994 . (1 + p)6 = N1994 . (1+0,046) . (1+0,039) . (1+0,038) . (1+0,057) . (1+0,049) . (1+0,033)
bzw. (1 + p)6 = (1+0,046) . (1+0,039) . (1+0,038) . (1+0,057) . (1+0,049) . (1+0,033)
und in weiterer Folge (1 + p) ist die sechste Wurzel daraus
bzw. 1 + p = 1,0436
Die durchschnittliche Wachstumsrate p beträgt somit 0.0436 = 4.36 %.
Übungsarbeit. 2-22:
![]()
Übungsarbeit 2-23:
(a) falsch
(b) falsch (Die Variablen müssen mindestens ordinalskaliert sein.)
(c) falsch
(d) falsch
(e) richtig
(f) richtig
(g) falsch (Der Median lässt keineswegs einen derartigen Schluss zu.)
(h) falsch
(i) richtig
(j) richtig